Surface Tension

Surface tension is a contractive tendency of the surface of a liquid that allows it to resist an external force. It is revealed, for example, in the floating of some objects on the surface of water, even though they are denser than water, and in the ability of some insects (e.g. water striders) to run on the water surface. This property is caused by cohesion of similar molecules, and is responsible for many of the behaviors of liquids.

Surface tension has the dimension of force per unit length, or of energy per unit area. The two are equivalent—but when referring to energy per unit of area, people use the term surface energy—which is a more general term in the sense that it applies also to solids and not just liquids.

In materials science, surface tension is used for either surface stress or surface free energy.

The cohesive forces among liquid molecules are responsible for the phenomenon of surface tension. In the bulk of the liquid, each molecule is pulled equally in every direction by neighboring liquid molecules, resulting in a net force of zero. The molecules at the surface do not have other molecules on all sides of them and therefore are pulled inwards. This creates some internal pressure and forces liquid surfaces to contract to the minimal area.

Surface tension is responsible for the shape of liquid droplets. Although easily deformed, droplets of water tend to be pulled into a spherical shape by the cohesive forces of the surface layer. In the absence of other forces, including gravity, drops of virtually all liquids would be perfectly spherical. The spherical shape minimizes the necessary "wall tension" of the surface layer according to Laplace's law.

Another way to view surface tension is in terms of energy. A molecule in contact with a neighbor is in a lower state of energy than if it were alone (not in contact with a neighbor). The interior molecules have as many neighbors as they can possibly have, but the boundary molecules are missing neighbors (compared to interior molecules) and therefore have a higher energy. For the liquid to minimize its energy state, the number of higher energy boundary molecules must be minimized. The minimized quantity of boundary molecules results in a minimized surface area.^[1]

As a result of surface area minimization, a surface will assume the smoothest shape it can (mathematical proof that "smooth" shapes minimize surface area relies on use of the Euler–Lagrange equation). Since any curvature in the surface shape results in greater area, a higher energy will also result. Consequently the surface will push back against any curvature in much the same way as a ball pushed uphill will push back to minimize its gravitational potential energy.

The cohesive forces between liquid molecules are responsible for the phenomenon known as surface tension. The molecules at the surface do not have other like molecules on all sides of them and consequently they cohere more strongly to those directly associated with them on the surface. This forms a surface "film" which makes it more difficult to move an object through the surface than to move it when it is completely submersed.

Surface tension is typically measured in dynes/cm, the force in dynes required to break a film of length 1 cm. Equivalently, it can be stated as surface energy in ergs per square centimeter. Water at 20°C has a surface tension of 72.8 dynes/cm compared to 22.3 for ethyl alcohol and 465 for mercury.

Liquid surface

The reason for this is that the pressure difference across a fluid interface is proportional to the mean curvature, as seen in the Young-Laplace equation. For an open soap film, the pressure difference is zero, hence the mean curvature is zero, and minimal surfaces have the property of zero mean curvature.To find the shape of the minimal surface bounded by some arbitrary shaped frame using strictly mathematical means can be a daunting task. Yet by fashioning the frame out of wire and dipping it in soap-solution, a locally minimal surface will appear in the resulting soap-film within seconds.

Examples of Surface Tension

Walking on water: Small insects such as the water strider can walk on water because their weight is not enough to penetrate the surface.

Floating a needle: A carefully placed small needle can be made to float on the surface of water even though it is several times as dense as water. If the surface is agitated to break up the surface tension, then needle will quickly sink.

Don't touch the tent!: Common tent materials are somewhat rainproof in that the surface tension of water will bridge the pores in the finely woven material. But if you touch the tent material with your finger, you break the surface tension and the rain will drip through.

Clinical test for jaundice: Normal urine has a surface tension of about 66 dynes/centimeter but if bile is present (a test for jaundice), it drops to about 55. In the Hay test, powdered sulfur is sprinkled on the urine surface. It will float on normal urine, but will sink if the surface tension is lowered by the bile.

Surface tension disinfectants: Disinfectants are usually solutions of low surface tension. This allow them to spread out on the cell walls of bacteria and disrupt them.

Soaps and detergents: These help the cleaning of clothes by lowering the surface tension of the water so that it more readily soaks into pores and soiled areas.

Washing with cold water: The major reason for using hot water for washing is that its surface tension is lower and it is a better wetting agent. But if the detergent lowers the surface tension, the heating may be unneccessary.

Why bubbles are round: The surface tension of water provides the necessary wall tension for the formation of bubbles with water. The tendency to minimize that wall tension pulls the bubbles into spherical shapes.

Surface Tension and Droplets: Surface tension is responsible for the shape of liquid droplets. Although easily deformed, droplets of water tend to be pulled into a spherical shape by the cohesive forces of the surface layer.

Cohesion and Surface Tension

The cohesive forces between molecules down into a liquid are shared with all neighboring atoms. Those on the surface have no neighboring atoms above, and exhibit stronger attractive forces upon their nearest neighbors on the surface. This enhancement of the intermolecular attractive forces at the surface is calledsurface tension

Cohesive forces are the intermolecular forces (such as those from hydrogen bonding and Van der Waals forces) which cause a tendency in liquids to resist separation. These attractive forces exist between molecules of the same substance. For instance, rain falls in droplets, rather than a fine mist, because water has strong cohesion which pulls its molecules tightly together, forming droplets. This force tends to unite molecules of a liquid, gathering them into relatively large clusters due to the molecules' dislike for its surrounding..

Adhesive forces are the attractive forces between unlike molecules. They are caused by forces acting between two substances, such as mechanical forces (sticking together) and electrostatic forces (attraction due to opposing charges). In the case of a liquid wetting agent, adhesion causes the liquid to cling to the surface on which it rests. When water is poured on clean glass, it tends to spread, forming a thin, uniform film over the glasses surface. This is because the adhesive forces between water and glass are strong enough to pull the water molecules out of their spherical formation and hold them against the surface of the glass, thus avoiding the repulsion between like molecules.

When liquid is placed on a smooth surface, the relative strengths of the cohesive and adhesive forces acting on that liquid determine the shape it will take (and whether or not it will wet the surface). If the adhesive forces between a liquid and a surface are stronger, they will pull the liquid down, causing it to wet the surface. However, if they cohesive forces among the liquid itself are stronger, they will resist such adhesion and cause the liquid to retain a spherical shape and bead the surface.

The Meniscus

Meniscus is the curvature of a liquid's surface within a container such as a graduated cylinder. However, before we explain why some liquid have a concave up meniscus while others share a concave down meniscus, first we have to understand the adhesive forces at work on surface tension.

Water, for example, is a polar molecule that consists of a partial positive charge on the hydrogens and a partial negative charge on the oxygen. Thus, within liquid water, each molecule's partial positive charge is attracted to its neighbor's partial negative charge. This is the origin of the cohesive forces within water. Water molecules buried inside the liquid is then being pulled and pushed evenly in every direction, producing no net pull. Meanwhile, the molecules on the surface of the liquid, lacking pulling forces in the upward direction thus encompass a net downward pull.

Two definitions

Surface tension, represented by the symbol γ is defined as the force along a line of unit length, where the force is parallel to the surface but perpendicular to the line. One way to picture this is to imagine a flat soap film bounded on one side by a taut thread of length, L. The thread will be pulled toward the interior of the film by a force equal to 2 $\scriptstyle\gamma$ L(the factor of 2 is because the soap film has two sides, hence two surfaces).

Surface tension is therefore measured in forces per unit length. Its SI unit is newton per meter but the cgs unit of dyne per cm is also used. One dyn/cm corresponds to 0.001 N/m.

An equivalent definition, one that is useful in thermodynamics, is work done per unit area. As such, in order to increase the surface area of a mass of liquid by an amount, δA, a quantity of work, $\scriptstyle\gamma$ δA, is needed.This work is stored as potential energy. Consequently surface tension can be also measured in SI system as joules per square meter and in the cgs system as ergs per cm². Since mechanical systems try to find a state of minimum potential energy, a free droplet of liquid naturally assumes a spherical shape, which has the minimum surface area for a given volume.

The equivalence of measurement of energy per unit area to force per unit length can be proven by dimensional analysis.

Surface curvature and pressure

Surface tension forces acting on a tiny (differential) patch of surface. δθ_xand δθ_y indicate the amount of bend over the dimensions of the patch. Balancing the tension forces with pressure leads to the Young–Laplace equation

If no force acts normal to a tensioned surface, the surface must remain flat. But if the pressure on one side of the surface differs from pressure on the other side, the pressure difference times surface area results in a normal force. In order for the surface tension forces to cancel the force due to pressure, the surface must be curved. The diagram shows how surface curvature of a tiny patch of surface leads to a net component of surface tension forces acting normal to the center of the patch. When all the forces are balanced, the resulting equation is known as the Young–Laplace equation:

$\Delta p\ =\ \gamma \left( \frac{1}{R_x} + \frac{1}{R_y} \right)$

where:

Δp is the pressure difference.
$\scriptstyle\gamma$ is surface tension.
R_x and R_y are radii of curvature in each of the axes that are parallel to the surface.

The quantity in parentheses on the right hand side is in fact (twice) the mean curvature of the surface (depending on normalisation).

Solutions to this equation determine the shape of water drops, puddles, menisci, soap bubbles, and all other shapes determined by surface tension (such as the shape of the impressions that a water strider's feet make on the surface of a pond).

The table below shows how the internal pressure of a water droplet increases with decreasing radius. For not very small drops the effect is subtle, but the pressure difference becomes enormous when the drop sizes approach the molecular size. (In the limit of a single molecule the concept becomes meaningless.)

Methods of measurement

Because surface tension manifests itself in various effects, it offers a number of paths to its measurement. Which method is optimal depends upon the nature of the liquid being measured, the conditions under which its tension is to be measured, and the stability of its surface when it is deformed.

Du Noüy Ring method: The traditional method used to measure surface or interfacial tension. Wetting properties of the surface or interface have little influence on this measuring technique. Maximum pull exerted on the ring by the surface is measured.Because surface tension manifests itself in various effects, it offers a number of paths to its measurement. Which method is optimal depends upon the nature of the liquid being measured, the conditions under which its tension is to be measured, and the stability of its surface when it is deformed.
Du Noüy-Padday method: A minimized version of Du Noüy method uses a small diameter metal needle instead of a ring, in combination with a high sensitivity microbalance to record maximum pull. The advantage of this method is that very small sample volumes (down to few tens of microliters) can be measured with very high precision, without the need to correct forbuoyancy (for a needle or rather, rod, with proper geometry). Further, the measurement can be performed very quickly, minimally in about 20 seconds. First commercial multichannel tensiometers were recently built based on this principle.

Wilhelmy plate method: A universal method especially suited to check surface tension over long time intervals. A vertical plate of known perimeter is attached to a balance, and the force due to wetting is measured.

Spinning drop method: This technique is ideal for measuring low interfacial tensions. The diameter of a drop within a heavy phase is measured while both are rotated.

Pendant drop method: Surface and interfacial tension can be measured by this technique, even at elevated temperatures and pressures. Geometry of a drop is analyzed optically. For details, see Drop.

Bubble pressure method (Jaeger's method): A measurement technique for determining surface tension at short surface ages. Maximum pressure of each bubble is measured.

Drop volume method: A method for determining interfacial tension as a function of interface age. Liquid of one density is pumped into a second liquid of a different density and time between drops produced is measured.

Capillary rise method: The end of a capillary is immersed into the solution. The height at which the solution reaches inside the capillary is related to the surface tension by the equation discussed below.

Stalagmometric method: A method of weighting and reading a drop of liquid.

Sessile drop method: A method for determining surface tension and density by placing a drop on a substrate and measuring the contact angle (see Sessile drop technique).

Vibrational frequency of levitated drops: The natural frequency of vibrational oscillations of magnetically levitated drops has been used to measure the surface tension of superfluid⁴He. This value is estimated to be 0.375 dyn/cm at T = 0 K.

Liquid in a vertical tube

Diagram of a mercury barometer

An old style mercury barometer consists of a vertical glass tube about 1 cm in diameter partially filled with mercury, and with a vacuum (calledTorricelli's vacuum) in the unfilled volume (see diagram to the right). Notice that the mercury level at the center of the tube is higher than at the edges, making the upper surface of the mercury dome-shaped. The center of mass of the entire column of mercury would be slightly lower if the top surface of the mercury were flat over the entire crossection of the tube. But the dome-shaped top gives slightly less surface area to the entire mass of mercury. Again the two effects combine to minimize the total potential energy. Such a surface shape is known as a convex meniscus.

The reason we consider the surface area of the entire mass of mercury, including the part of the surface that is in contact with the glass, is because mercury does not adhere at all to glass. So the surface tension of the mercury acts over its entire surface area, including where it is in contact with the glass. If instead of glass, the tube were made out of copper, the situation would be very different. Mercury aggressively adheres to copper. So in a copper tube, the level of mercury at the center of the tube will be lower than at the edges (that is, it would be a concave meniscus). In a situation where the liquid adheres to the walls of its container, we consider the part of the fluid's surface area that is in contact with the container to have negativesurface tension. The fluid then works to maximize the contact surface area. So in this case increasing the area in contact with the container decreases rather than increases the potential energy. That decrease is enough to compensate for the increased potential energy associated with lifting the fluid near the walls of the container.

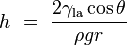
$h\ =\ \frac {2\gamma_\mathrm{la} \cos\theta}{\rho g r}$

If a tube is sufficiently narrow and the liquid adhesion to its walls is sufficiently strong, surface tension can draw liquid up the tube in a phenomenon known as capillary action. The height the column is lifted to is given by:

where

$\scriptstyle h$ is the height the liquid is lifted,
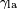$\scriptstyle \gamma_\mathrm{la}$ is the liquid-air surface tension,
$\scriptstyle \rho$ is the density of the liquid,
$\scriptstyle r$ is the radius of the capillary,
$\scriptstyle g$ is the acceleration due to gravity,
$\scriptstyle \theta$ is the angle of contact described above. If $\scriptstyle \theta$ is greater than 90°, as with mercury in a glass container, the liquid will be depressed rather than lifted.

Capillary attraction

Capillary attraction, or capillarity, is the ability of a liquid to flow in narrow spaces without the assistance of, and in opposition to external forces like gravity. The effect can be seen in the drawing up of liquids between the hairs of a paint-brush, in a thin tube, in porous materials such as paper, in some non-porous materials such as liquified carbon fiber, or in a cell. It occurs because of inter-molecular attractive forces between the liquid and solid surrounding surfaces. If the diameter of the tube is sufficiently small, then the combination of surface tension(which is caused by cohesion within the liquid) and adhesive forces between the liquid and container act to lift the liquid.

Capillary action, capillarity, capillary motion, or wicking refers to two phenomena:

A common apparatus used to demonstrate the first phenomenon is the capillary tube. When the lower end of a vertical glass tube is placed in a liquid such as water, a concave meniscus forms. Adhesion forces between the fluid and the solid inner wall pulls the liquid column up until there is a sufficient mass of liquid for gravitational forces to overcome these intermolecular forces. The contact length (around the edge) between the top of the liquid column and the tube is proportional to the diameter of the tube, while the weight of the liquid column is proportional to the square of the tube's diameter, so a narrow tube will draw a liquid column higher than a wide tube.

Kimyasal Teorik Bilgiler ve Deneyler

15 Aralık 2012 Cumartesi

Surface Tension,Cohesion,Adhesive Force,Methods of Measurement